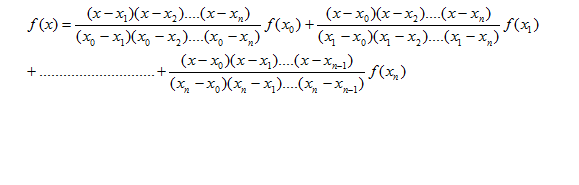Table of Contents
‘C’ program to implement Lagrange’s Interpolation formula.
Theory and Concept –
Interpolation formulae for equally Spaced Argument is important but as is well known they possess the disadvantage of requiring the values of the independent variable to be equally spaced. It is therefore desirable to have interpolation formulae with unequally space values of the argument. There are two such formulae:
1. Lagrange’s Interpolation formula –
Lagrange’s Interpolation formula uses only the function values. Lagrange’s Interpolation formula may be written as:
Program in C to Implement Lagrange’s Interpolation
#include
#include
#include
void main()
{
float x[10],y[10],temp=1,f[10],sum,p;
int i,n,j,k=0,c;
clrscr();
printf(“nhow many record you will be enter: “);
scanf(“%d”,&n);
for(i=0; i
{
printf(“nnenter the value of x%d: “,i);
scanf(“%f”,&x[i]);
printf(“nnenter the value of f(x%d): “,i);
scanf(“%f”,&y[i]);
}
printf(“nnEnter X for finding f(x): “);
scanf(“%f”,&p);
for(i=0;i
{
temp = 1;
k = i;
for(j=0;j
{
if(k==j)
{
continue;
}
else
{
temp = temp * ((p-x[j])/(x[k]-x[j]));
}
}
f[i]=y[i]*temp;
}
for(i=0;i
{
sum = sum + f[i];
}
printf(“nn f(%.1f) = %f “,p,sum);
getch();
}
/*
______________________________________ OUT PUT
______________________________________
______________________________________ OUT PUT
______________________________________
how many record you will be enter: 4
enter the value of x0: 0
enter the value of f(x0): 0
enter the value of x1: 1
enter the value of f(x1): 2
enter the value of x2: 2
enter the value of f(x2): 8
enter the value of x3: 3
enter the value of f(x3): 27
Enter X for finding f(x): 2.5
f(2.5) = 15.312500
*/
Keywords: Lagrange’s Interpolation formula, Program in C to implement Lagrange’s formula
