What is AVL Tree ?
AVL stands for ADELSON, VELSKI AND LANDIS. It is a tree representation commonly known as ‘AVL TREE’.Here we have explained an avl tree example in the figure. AVL tree is just like a binary search tree(BST) but it is a balanced tree in data structure. Here the the term balanced is used in context of height it means AVL Tree is a height balanced tree.in data structure. It is heught balanced binary search tree.If in binary search tree, at every node avl tree balance factor is 1 or 0 or -1, then it is AVL tree.
Balancing factor of a node in VAL tree is calculated using this formula
Balancing factor = (height of left sub tree) – (height of right sub tree)
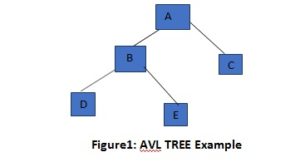
An avl tree example is given below
In the above avl tree example the balance factor of node A is 1 and balance factor of node B, C,Dand E is 0.
Why do we need AVL Trees?
If the height of binary search tree is h then most of the BST operations take O(h) time to perform. So if, we manage the height of the tree remains O(logn) after every insertion and deletion, then the upper bound will beO(logn) for all BSToperations.The height of an AVL tree is always O(logn) where n is the number of nodes in the tree. Hence, it has complexity of O(logn).
How can a tree be represented as AVL tree?
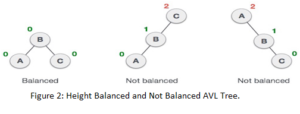
Let us take tree representation as
In the first representation, tree is balanced as it has left subtree height and right subtree same. In second representation node A and node B is balanced as they have avl tree balance factor as 0 and 1 respectively whereas, node C is not balanced, Hence complete tree is not balanced. Similarly, in case of third representation it is not a balanced tree in data
AVL Tree Rotations with Example
To make unbalanced tree as balanced tree we need to apply some rotations on the tree .Some avl tree rotations example are as follows
1. Left rotation
2. Right rotation
3. Left-Right rotation
4. Right-Left rotation
First and second rotations are single rotations and the next two rotations are double rotations.
NOTE:- To represent unbalanced tree we atleast need height as 2.
Left Rotation
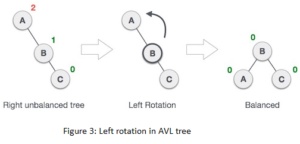
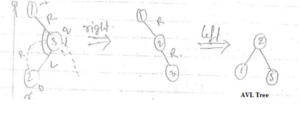
When a node is inserted into the right subtree of the right sub tree then it become unbalanced. Then this problem is known as “RR- PROBLEM” and to make it balanced we perform a left rotation. An avl tree rotation example for left rotation is explained below.
Left Rotation(RR Problem)
In our example, load factor of node A is 2 so it is unbalanced as a node is inserted in the right subtree of A’s right subtree. SO in order to make the tree balanced we perform the left rotation by making A the left-subtree of B.
Right Rotation
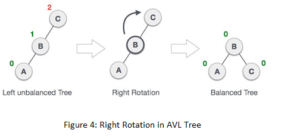
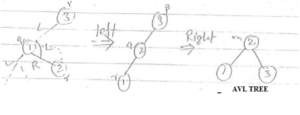
When a node is inserted in the left subtree of the left subtree of Root Node then it become unbalanced. This problem is known as “LL-PROBLEM” and to balance this tree we perform a right rotation. An avl tree rotation example for right rotation is explained below.
Right Rotation(LL Problem)
As depicted, the unbalanced node becomes the right child of its left child by performing a right rotation.
LEFT RIGHT ROTATION(LR)
If we insert a node in right of left subtree of root node then it become unbalanced then we performed Left Right rotation. Here is avl tree rotation example for left right rotation.
As Shown in above figure When we insert a node in the right of node q then it become unbalanced. Here in this case we need to perform two rotation as shown in figure to meake the tree balanced.
When a new node is inserted in the left of right sub tree of node P as shown in following figure. Here also we need to perform two rotation. Here is avl tree rotation example for right left rotation.
In the next post we will learn about insertion and deletion in AVL Tree.
