Table of Contents
TOC Questions for GATE Exam Practice
Some important theory of computation tutorial questions and toc gate questions for practice for the gate exam cse aspirants. Here toc gate questions from different topic in automata theory such as dfa questions ,and regular expression questions in automata has been covered in this practice set.
Computer science students are advised to practice and learn theory of computation tutorial as per syllabus of gate cse syllabus 2021 before attempt these
Questions and Answers
A computer science graduate should have the knowledge about following questions and answer or the concepts in order to attempt these toc gate questions.
- Concepts of DFA
- Concepts of NFA
- Regular Expression in automata.
- What is Context Free Language ?
- What is Grammar in theory of automata ?
Note – Don’t forget to study Views in SQL
Theory of Computation Tutorial for GATE
Here in this theory of computation tutorial we have discussed some previous year toc gate questions with their answer.
Q1. Consider S and T be languages over ={a,b} and these are represented by the given regular expressions (a+b*)* and (a+b)*, respectively. Then find the correct statement among the following (GATE CS 2000)
(a) S is a subset of
(b) T is a subset of S
(c) S=T
(d) S ∩T=Ø
Answer: (c).
2.A language L denotes the language generated by the grammar S – OSO/00. Then find the correct statement? (GATE CS 2000)
(a) L = O+
(b) L is regular but not O+
(c) L is context free but not regular
(d) L is not context free
Answer: (b)
3.Consider the following two statements:
S1: { 0^2n |n >= l} is a regular language
S2: { 0^m 0^n 0^(m+n) l m >= 1 and n >= 2} is a regular language
Which is true ? (GATE CS 2001)
a) Only S1 is correct
b) Only S2 is correct
c) Both S1 and S2 are correct
d) None of S1 and S2 is correct.
Answer: (c)
- Find the correct statement among the following? (GATE CS 2001)
(a) If a language is context free it can always be accepted by a deterministic push-down automaton
(b) The union of two context free languages is context free
(c) The intersection of two context free languages is context free
(d) The complement of a context free language is context free
Answer: (b)

TOC Questions for GATE Exam Practice
Here in this sections we have discussed some toc questions for gate exam practice with their solution and answer.
1. Number of trivial substrings in “GATE2013” are:
(a) 37 (b) 35
(c) 2 (d) 36
2. Let the string be defined over symbols a and b then what will be the number of states in minimal DFA, if every string starts and ends with different symbols?
(a) 5 (b) 4
(c) 3 (d) None
3. The total number of substrings present in “GATE” is:
(a) 7 (b) 10
(c) 11 (d) 8
4. Let Σ= {a, b}, what are the number of states in minimal DFA, length of every string congruent
to mod 5.
(a) 2 (b) 3
(c) 5 (d) None
5. A minimal DFA that is equivalent to a NDFA has:
A. Always more states (b) Always less no. of states
C. Exactly 2n states (d) Sometimes more states
Also Practice – Computer Networks Gate Questions and Answers
6. Consider following Regular Expression:
(i) a*b*b (a+ (ab)*)* b*
(ii) a*(ab + ba)* b*
Find the length of shortest string which is in both (i) & (ii)?
(a) 2 (b) 3
(c) 4 (d) None
7. S àAB
Aà BB/ a
Bà AB/ b
Choose incorrect statement?
A. aabbb can be derived from above grammar
B. aabb can be derived from above grammar
C. ababab can be derived from above grammar
D. abbb can be derived from above grammar

8. One of the following Regular Expressions is not the same as others. Which one?
(a) (a* + b*a*)* (b) (a*b* + b*a*)* (a*b*)*
(c) ((ab)* + a*)* (d) (a + b)* a*b*a*b*
9. The complement of CFL:
(a) Recursive (b) Recursive enumerated
(c) Not RE (d) The empty set
10. The language of primes in unary is:
(a) Regular (b) CFL
(c) DCFL (d) Context Sensitive
11. Consider the regular grammar generating the set of all strings ending with ‘00’, with terminals {0,1} and non-terminals {S, A, B}, S being the initial state and B, the final state.
S–> 1/ 0 →0
→0/1/0
The production missing is
(a) →1 (b) →
(c) →1 (d) →1
12. What are the number of states needed in minimal DFA, that accepts (1+1111)*, with 1 as alphabet here.
(a) 5 (b) 4
(c) 1 (d) None
Also Practice – Dbms Gate Questions and Answers
13. Consider the grammar:
SàaSbS/ bSaS/ ε,
Which one among the following is the smallest which has twp deviation trees.?
(a) abab (b) aabb
(c) bbaa (d) aaabbb
14. The language L= { aNbN/ 0< N < 327th Prime number} is
(a) Regular (b) Not context sensitive
(c) Not recursive (d) None
15. Consider the set of input Σ= {a},
And assume language, L= {a2012.K/ K> 0},
Which among the following is the value of minimum number of states that is needed in a DFA to recognize the given language L?
(a) 22012 + 1 (b) 2013
(c) 22013 (d) None
Also Practice – Computer Organization Gate Questions and Answers
16. The following CFG,
Sà aB/ bA
Aà a/ aS/ bAA
Bà b/ bS/ aBB generates strings with
(a) Odd number of a’s & odd number of b’s
(b) Even number of a’s & even number of b’s
(c) Equal number of a’s & b’s
(d) Odd number of a’s & even number of b’s
17. What type of grammar is this most accurately described as?
Sàb/aD
Dà a/aDD
(a) A regular grammar (b) CFG
(c) CSG (d) Type-0
18. Consider the following NFA M over the alphabet {0,1}.
Let M1 be the NFA obtained by interchanging final and non-final states of M. Let the language accepted by M be L and that accepted by M1 be L1. Choose correct statement:
(a) L1= L (b) L1∩ L2= Φ
(c) L1⊆ L2 (d) L1= (0+1)*
19. Let M= (Q, Σ, δ, S, F) and M’= (Q, Σ, δ, S, Q – F) where M accepts L and M’ accepts L1 and M is NFA, which among the following is the relation between L and L’ ?
(a) L and L’ are complement to each other
(b) L and L’ are similar to each other
(c) L and L’ relation cannot be predicted
(d) None of the above
Answer Sheet and Explanation
The answers and explanation of the solution for the questions as discussed in above theory of computation tutorial are given below
- Solution: Option (c)
Explanation:
For any string, there will always be only 2 trivial substrings, ∈ and the given string itself.
2.Solution: Option (a)
3.Solution (c)
4.Solution: Option (c)
5.Solution: Option (d)
6.Solution: Option (d)
Explanation: The shortest string is generated by both the regular expressions
- Solution: Option (b)
- Solution: Option (c)
Explanation: abb cannot be generated by C, whereas it is generated by all other regular expressions.
- Solution: Option (a)
- Solution: Option (d)
Explanation:
The language of primes in unary is {1/ }. Finite automata cannot recognize this language as it has no memory. Push Down Automata also cannot recognize this because there is no pattern in the strings that can be remembered using one stack. LBA can accept this, so it is a context sensitive language.
- Solution: Option (a)
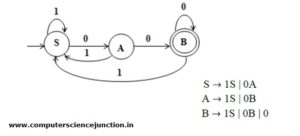 12: Option (c)
12: Option (c)
Explanation: The language is 1*.
- Solution: Option (a)
- Solution: Option (a)
Explanation: Since this is finite language, it is regular.
- Solution: Option (b)
![]() 16. Solution: Option (c)
16. Solution: Option (c)
17.Solution: Option (b)
Explanation:
(a) This cannot be regular because regular grammars are of the form →,→
(b) It is CFG because all the productions satisfy the constraints, they are of the form → where is a string of terminals and/or non-terminals.
(c) It can be CSG because all the productions are of the form →, where ,, are strings of terminals and/or non-terminals.
(d) It can be Type – 0 or unrestricted grammar, because all productions are of the form → (no restrictions).
But it can be most accurately described as CFG.
- Solution: Option (d)
Explanation:
If we interchange final and non-final states then we get 1=(0+1)∗.
19.Solution: Option (c)
- Solution: Option (b)
- Solution: Option (a)
Explanation:
Consider the grammar given below where the flowers are non-terminals and animals are terminals:
→/ / /
In this a is used for tiger and b is used for lion, X is used for Flowers.
- Solution: Option (b)
- Solution: Option (d)
Give your feedback in comment section. If you like this post then please follow us on social media.
Other important link related toc study material are as follow
- Click Here for second theory of computation tutorial
Recommended Post – Implementation of Fibonacci Series in Python
Some Important Points in TOC
Remember some tips or important points in automata theory or theory of computation for gate exam. These point are as shown in figure given below

I kindly request to readers please give your feedback and suggestion. If you find any mistake in this theory of computation tutorial then comment.
If you want to add or contribute some more information to this tutorial then mai us at the email id computersciencejunction@gmail.com
Don’t stop learning and practice.
If you find this page useful then please Like and Share the post on Facebook, Twitter, Linkedin through their icons as given below.


