Table of Contents
Theory of Computation Gate Questions for Practice
Theory of computation gate questions for practice are discussed here in this post. These theory of computation gate questions are on finite automata and regular language topics of Theory of Computation. I hope that these theory of computation gate questions will be helpful for gate exam aspirants.

Latest Update – GATE 2021 CSE Question Paper and Solution
Questions 1. r1 = 1 (0 + 1)* r2 = 1 (1 + 0)+ r3 = 1 1* 0
Which one Relation is correct ?
| (a) L (r1) ⊆ L (r2) and L(r1) ⊆ L(r3) | (b) L (r1) ⊇ L (r2) and L(r2) ⊇ L(r3) |
| (c) L (r1) ⊇ L (r2) and L(r2) ⊆ L(r3) | (d) L (r1) ⊆ L (r3) and L(r2) ⊆ L(r1) |
Question 2.Give the strongest correct statement about finite language over finite Ʃ ?
(a)It could be undecidable
(b)It is Turing-recognizable
(c)It is CSL
(d)It is regular language
Question 3. If there are n1 number of states in a minimal NFA of a language and n2 states are there I DFA the what is relation between n1 and n2. Relation?
| (a) n1 | ≥ n2 | (b) n1 | ≤ n2 |
| (c) n1 | < n2 | (d) n2 | > n1 |
Question 4.
S1: L is regular. Infinite union of L will also be regular i.e. (L0 ∪ L1 ∪ L2 . . .)
S2: L is regular. It’s subset will also be regular.
| (a) Both are true | (b) Both are false |
| (c) S1 → T, S2 → F | (d) S1 → F, S2 → T |
Question 5. There is a regular expression r = (11 + 111)* over Ʃ = {0, 1}. Then what are the number of states in minimal NFA and DFA.
| (a) N – 3, D – 4 | (b) N – 3, D – 3 |
| (c) N – 3, D – 3 | (d) N – 4, D – 4 |
Question 6.A Language is said to be regular iff
(a)There is Regular Grammar which right linear for L
(b)There is Regular Grammar which is left linear for L
(c)There exists a nfa with single final state
(d)There exists a dfa with single final state
(e)There exists a nfa without ԑ – move
| Which are true? | |
| (i) All are true | (b) a, b, c are true |
| (c) all are true except d. | (d) a, b, d are true |
Question 7. There 2 cases
Case1: For DFA (ϕ, Ʃ, δ, qo, F), if F = ϕ, then L = Ʃ*
Case2: For NFA (ϕ, Ʃ, δ, qo, F), if F = ϕ, then L = Ʃ*
Where F = Final states set
ϕ= Total states set
| (a) Both are true | (b) Both are False |
| (c) Case1 is true, Case2 is false | (d) Case1 is false, Case2 is true |
Question 8.Consider this FA:
What are the number of strings in the complement of the language accepted by this Finite Automata?
| (a) Infinite | (b) 2 |
| (c) 3 | (d) 0 |
Question 9. In Programming language, an identifier has to be a letter followed by any number of letters or digits. If L and D denotes the sets of letter and digits respectively, examine the correct expressions?
| (a) (L ∪ D)* | (b) (L ∙ D)* |
| (c) L ∙ (L ∪ D)* | (d) L ∙ (L ∙ D)* |
| Question 10. | |
| Ʃ = {0, 1} | |
| L = Ʃ* | |
| R = { On 1n such that n > 1} | |
| Languages L ∪ R and R are respectively: | |
| (a) Regular, Regular | (b) Regular, Not Regular |
| (c) Not Regular, Not Regular | (d) Not Regular, Regular |
Question 11.
L1 = { am | m ≥ 0}
L2 = { bm | m ≥ 0}
| L1 ∙ L2 = ? | |
| (a) { am bm, m ≥ 0} | (b) {am bn, m, n ≥ 0} |
| (c) {am bn, m, n ≥ 1} | (d) None of the above |
Question 12.Consider these statements:
Statement1: If a language is infinite, it has to be non-Regular.
Statement2: Let L be any language.
| (L)∗ ≠ (L∗) | |||
| (a) Both are True | (b) Both are False | ||
| (c) S1 → True, S2 → False | (d) S1 → False, S2 → True | ||
| 3 | |||
Question 13.Which of the following set can be recognized by DFA?
(a)Numbers 1, 2, 4, 8, . . . 2n written in binary
(b)Numbers 1, 3, 4, 8, . . . 2n written in unary
(c)Set of binary strings in which number of zeroes is same as number of 1’s
(d)Set {1, 101, 11011, 1110111, . . .}
Solution and Explanation
- Solution: Option (b)
- Option d
- Option b
4.Option (b)
Explanation:
For Statement 1:
Regular languages are closed under finite union. They are not closed under infinite union of regular languages.
Consider 1={01} 2={0212} 3={0313}
So, infinite union of 1∪2∪3∪…={(01)/(>0)} is CFL but not regular.
- Option (a)
Explanation: The language for the given regular expression is ={,11,111,1111,11111,…}. So the DFA is
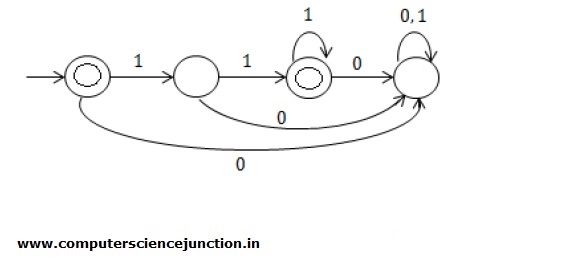
- Solution: Option (iii)
Explanation:
Since a DFA having multiple final states cannot be converted to DFA with a single final state.
7.Solution: Option (c)
Explanation:
As in case of NFA even is F = ϕ, dead state rejection is there so L ≠ Ʃ*.
8.Solution: Option (d)
Explanation: As L is (a + b)*
L = { }
9.Solution: Option (c)
- Solution: Option (a)
- Solution: Option (b)
Explanation:
L ∪ R → Regular
R → CFL
- Solution: Option ( b)
- Solution: Option (d)
Explanation:
Infinite can also be regular → ∗
(L)∗ will surely contain ∈
but (L∗) will not contain ∈.
So, they are not equal
Conclusion and Summary
Here in this post we have discussed some theory of computation questions for GATE exam with their solution.
I kindly request to readers please give your feedback and suggestion. If you find any mistake in this tutorial then comment.
Don’t stop learning and practice.
More – Theory of Computation Gate Practice Questions.


