Binary Tree and its Types in Data Structure

• In this tutorial we will learn about Binary Tree and its Types in data structure.
• Every type of binary tree  has it’s specific characteristics.
• We can identify the type of tree on the basis of this characteristics.

Some time types of binary tree based multiple choice questions are asked in the GATE(CS)/UGC NET exam, therefore it is important for a computer science student to understand the properties of binary tree and types of binary tree.

Here in this tutorial we explained properties of tree and different types of tree with proper diagram. This tutorial will be beneficial for computer science students.

Let’s start with Introduction of Tree Data Structure.

Frequently Asked Questions

After reading this tutorial students will be able to answer the frequently asked questions in technical interview from this topic. These frequently asked questions are as follow

• What is Tree Data Structure ?
• What is Binary Tree ?
• What are different types of binary tree ?
• What are different properties of binary tree ?
• What is difference between full binary tree and complete binary tree?y tree ?
• What is the maximum number of leaf nodes in a binary tree of height h?
• How many leaf nodes are in a binary tree with n nodes?
• What is depth in binary tree?
• What is the minimum height height of a full binary tree?
• What is depth and height of a tree?

Let’s start with introduction of tree data structure.

What is Tree in Data Structure ?

• Tree is a non linear data structure which represents data in hierarchical form.
• For example, if we take the employees of an organization, they can be viewed in a hierarchical order.

The organizational hierarchy of the company would look like-

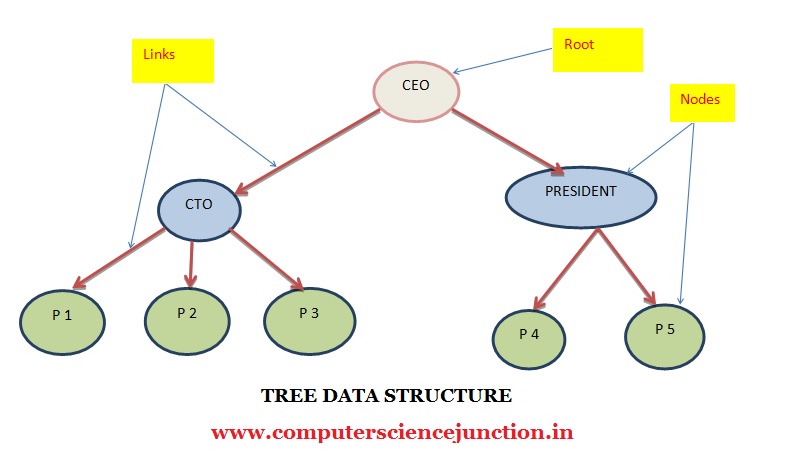
Here, the CEO has two direct reports CTO and the President. And CTO is the manager of P1, P2 and P3 and President is the manager of P4 and P5.

This particular logical structure resembles a tree. The root is at the top of it and it is branching out downwards.

Tree is an efficient way of storing and organizing data that is hierarchical in nature. Tree data structure can be defined as a collection of nodes which are linked together to reproduce a hierarchy.

The topmost node in the tree is called a root. Each node in the tree contains some data. In the above example the type of data in each node is the designation of employees in a particular company.

Each node may also contain some link or reference to other nodes that can be called as the children nodes. Let’s focus on the figure below

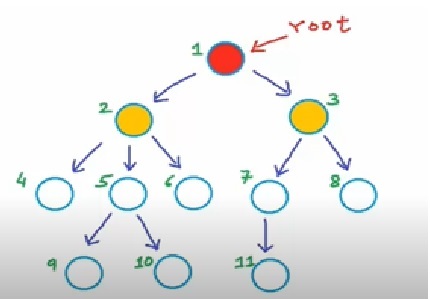
In the above figure, the root node or node 1 is directly linked to nodes 2 and 3. Hence 2 and 3 are the child nodes of node 1 and node 1 is the parent node of nodes 2 and 3. Root is the only node which does not have a parent.

Children of same parent are called siblings.

Here, 2 and 3 are siblings. Also 4, 5 and 6 are also siblings. Any node that doesn’t have a child node is called a leaf node. Here nodes 6, 8, 9, 10 and 11 are leaf nodes

The links in the tree are one-directional. Here, we can go from 1 to 2 and 3. Hence 1 is called the ancestor of 2 and 3; while, 2 and 3 are called the descendent of 1.

What are the Properties of Tree ?

Various properties of tree data structure have been explained in this section.

1.Recursive Data Structure

Trees have a distinguished node called root and also some sub-trees and the arrangement is such that the root of tree contains the links to the roots of all the sub-trees.

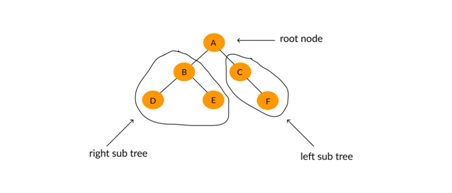
2. A tree with N numbers of nodes has exactly N-1 no. of links or edges. All nodes except the root node have exactly one incoming link or edge each.

3. Depth and Height of a Node in Tree

Depth of a node x in a tree is defined as length of path from root to x or, number of edges from root to x. The depth of root node is always 0.

Height of a node x in tree is defined as the number of edges in the longest path from x to leaf

In the above figure, depth of D, E and F is 2. Similarly depth of B and C is 1 and of A is 0.

The height of node C is 1 as the longest path from C is a leaf node F is 1. Similarly height of A is 2 as the longest path of A to a leaf node D is 2.

Key Point – Height of a tree is defined as the height of the root node. Here in the above figure the height of the tree is 2.

What is Binary Tree ?

• Based on properties of the trees, the trees are further classified into various categories.
• The simplest and most common kind of tree is a binary tree.
• Binary tree is the tree where any node can have at most 2 children.

One example of binary tree is depicted below-

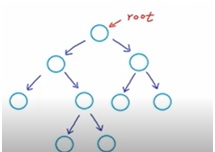
Here each node has two children. A node can have 1 child but can’t have more than 2 children. The child to the left is called left-child and child to the right is called right-child.

If a tree has just one node then also it’s a binary tree.

Terminology Used in Binary Tree

Following terms are generally used in Binary Tree.

Node –  Node Contains a Data Value in Binary tree.

Root – Top most node in the tree is known as root of tree

Parent – A node in a tree that has a child is known as Parent node.

Child – A node that came from a parent node moving away from root is known as child.

Leaf Node – A node with no child is know as leaf node of the tree. Leaf node is also known as external node.

Internal Node- These are the inner node at least one child.

Depth of a node Tree – Depth  is calculated in context of a specific node. Number of edges from a specific node to the root is known as depth of that node in tree. Depth of root node will be zero.

Height  of Node in Tree – Height of a node is the number of edges from that node to the deepest leaf node of the tree.  Height of Root will be maximum as compare to height of other nodes in the tree.

Different Types of Binary Tree

There are following types of binary tree exist in data structure. Different types of Binary Tree are explained in this section.

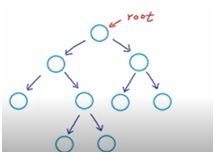
1.Strict Binary Tree

Strict Binary tree is also known as proper binary tree. In a strict or proper binary tree each node can have either 2 or 0 children. A strict binary tree is shown below-

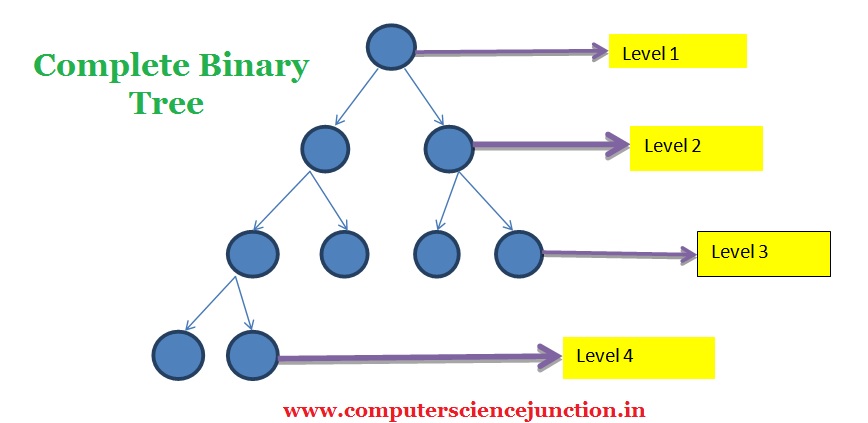
2.Complete Binary Tree

In a complete binary tree, all the levels except possibly the last are completely filled and all nodes are as left as possible. A complete binary tree is shown below-

In the above tree, there are 4 levels. If there no. of levels in a tree then the maximum no. of nodes in the level is .

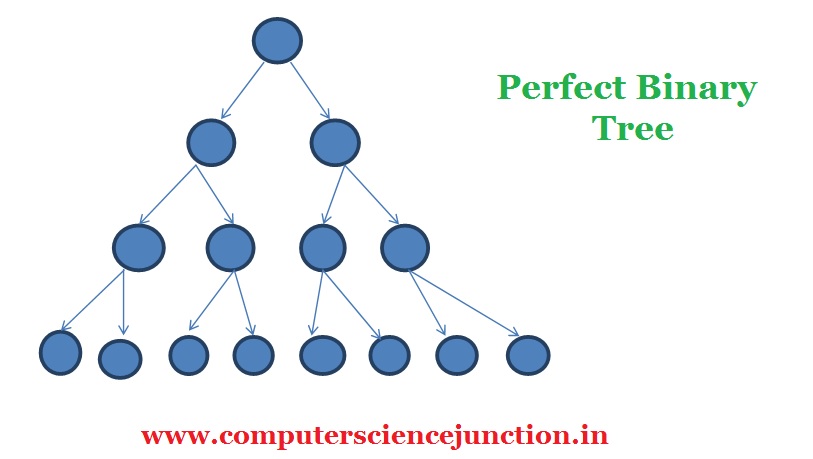
3.Perfect Binary Tree

In a perfect binary tree all levels will be perfectly filled. A perfect binary tree is shown below-

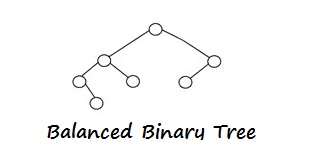
4.Balanced Binary Tree

A balanced tree is a tree with Hight O( log N) . Where N is the number of nodes in the tree.  Maximum difference of height of a left sub tree and right sub tree should be 1 in a a balanced Tree. but this difference may 0,-1 or 1. Balanced tree is also known as AVL tree.

Balanced Binary Tree is as shown in following figure –

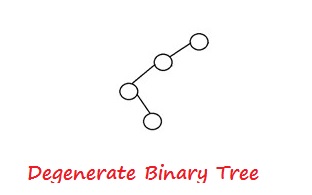
5. Degenerate Binary Tree

A binary tree is said to be a degenerate binary tree or some time pathological binary tree if every internal node of the tree has only a single child. A Degenerate tree is as shown in following figure.

 

Conclusion and Summary

We have explained the Binary Tree and It’s Types in this tutorial.

I hope this types of binary tree based tutorial will be beneficial for computer science students.

Your feedback is precious to us. Please give your feedback or leave a comment to improve the quality of our tutorials and provide tutorials as per your expectation.

If you find this page helpful, then please Like and Share the post on Facebook, Twitter, LinkedIn through their icons as given below.

Do not stop learning and practice.

Previous Tutorial – Tree Traversal in Data Structure

Next Tutorial – Binary Search Tree