Table of Contents
Binary Search Tree Tutorial
- A Binary Search Tree is a special type of Binary Tree in which every node has a key or value associated with it which is less than the key of each node in it’s right sub tree and greater than the key of node in it’s left sub tree.
Questions based on binary search tree are generally asked in various competitive examination such as GATE(CS), UGC NET, ISRO, DRDO etc.
In this tutorial we have explained the concepts of binary search tree with suitable examples.
Insertion operation in Binary Search Tree is also explained with example.
Process of deleting a node in binary search tree is also explained in this tutorial with examples.
I kindly request to computer science students to read this Binary Search Tutorial tutorial completely.
Frequently asked Questions
If you are preparing for GATE(CS), UGC NET or you are applying for the job such as Software developer then your written test or technical interview may contains several questions based on Binary Search Tree concepts.
Most Frequently asked questions from binary search tree are as follow –
- What is Binary Search Tree ?
- How do you delete a node from Binary Search Tree?
- How to convert binary tree in to Binary Search Tree ?]
- How to create a binary search tree from a list of numbers ?
Let’s Start with Introduction of Binary Search Tree
What is Binary Search Tree ?
Binary Search Tree owns properties of the tree data structures, the trees are further classified into various categories.
The simplest and most common kind of tree is a binary tree. Binary tree is the Tree Data Structure where any node can have at most 2 children.
A binary tree is drawn below-
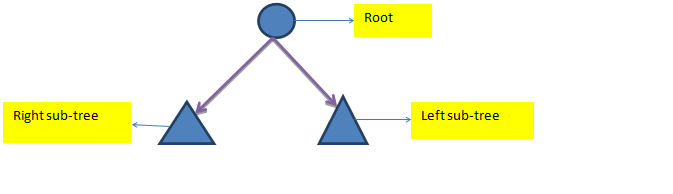
Key Point to Remember – Binary search tree is a special kind of binary tree which is an efficient structure, to organize data for quick search as well as quick update.
A Binary search tree is a special kind of Binary Tree where for each node, value of all the nodes in the left sub-tree is lesser or equal and value of all nodes in the right sub-tree is greater.
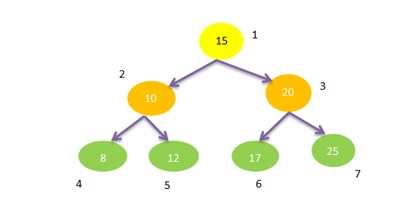
Let’s look at the figure below. It is a binary tree of integers.
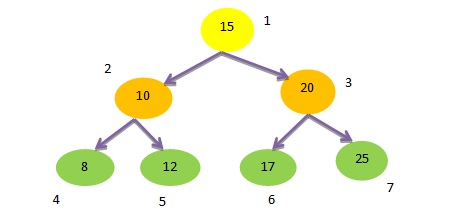
- In the above figure, node 1 is the root node with value 15.
- The values in left sub-tree are 10, 8 and 12 which are less than 15. In the right sub tree the values are 20, 17 and 25 which are greater than 15. This fulfills the condition for binary search tree.
- Again if we take node 2 as a root node 4 is its left child (value=8<10) and node 5 is its right child (value=12>10). This also fulfills the condition for binary search tree.
So given tree is a Binary Search Tree.
- Now if we have a modifiable data structure, after storing the modifiable collection in computer’s memory we should be able to search data, insert new data and delete existing data.
- We can perform these operations in a binary search tree very easily efficiently. Let’s take a look at that.
Search Operation in Binary Search Tree
If we want to find that a given key is or node exist in binary search tree or node than we use the following steps to perform search operation in Binary Search Tree.
Step 1 – First we compare the key or node to be searched with the root node. If it match than print search is successful and element is present in binary search tree.
Step 2 – If key of node to be search is smaller than root than we will search in left sub tree and compare with each node in left sub tree. If it match with any node then print search is successful.
Step 3 – If key of node to be search is greater than root than we will search in right sub tree and compare with each node in right sub tree. If it match with any node then print search is successful.
Example – In the above Binary Search Tree we have to find 10 is present or not.
If the element to be searched is less than the root node the search space will be reduced to the left sub tree and if it is greater than the root, then the search space is reduced to the right sub tree of the binary search tree.
Here 10<15, hence the search space is the left sub tree.
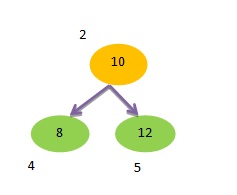
In the left sub-tree, we will first compare the element to be searched with the root of the left sub-tree.
If the element to be searched matches the root then we have found the element.
But if it is less we’ll search in the left side and if it is greater we’ll search in the right side of the tree.
Here the element to be searched matches the root of the left sub-tree and we have found 10.
Note – For a tree having n nodes, we’ll start the search space with n nodes and till we find the element we’ll go on reducing the search space by n/2 then n/4 and so on till we find the element.
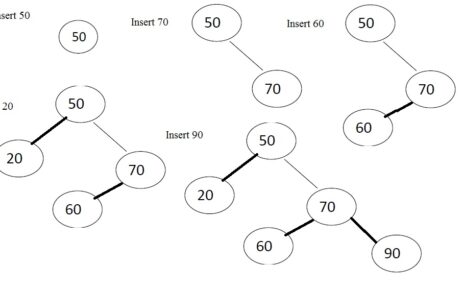
Insertion in Binary Search Tree
Insertion in Binary Search Tree has the same concept as search operation. Algorithm to perform insertion in Binary Search Tree has the following steps.
Step 1 – First we compare the key or node to be insert with the root node. If key of node to be insert is smaller than root than node will be insert in left sub tree. We will compare with each node in left sub tree and insert the node at appropriate location in left sub tree.
Step 2 – If key of node to be insert is greater than root than node will be inserted into right sub tree. We will compare with each node in left sub tree and insert the node in right sub tree and insert the node at appropriate location in right sub tree.
In the next section of this Binary Search Tree Tutorial we will learn about deletion operation in Binary Search Tree.
Deletion in Binary Search Tree
When we perform deletion operation in Binary Search Tree then there are three possible case
If we delete a node from a BST, 3 cases may appear-
- The node to be deleted that has no child.
- The node to be deleted has 1 child.
- The node to be deleted has 2 children.
Let’s discuss all three conditions one by one.
The figure below shows a BST.
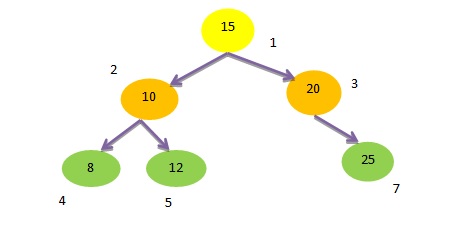
Case 1 : If deleting a node having 0 child or no child
Concept – If we want to delete a node which has no child then we simply delete that node from Binary search Tree.
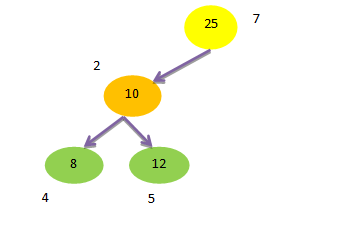
Example – For example Node 7 having value 25 is has 0 child. Let’s consider we want to delete that node.
In that case we can simply delete the left link to node 3, which gives us the tree below-
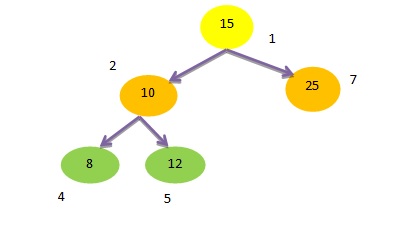
 Case 2: If The node to be deleted have one child
Case 2: If The node to be deleted have one child
Concept – If we want to delete a node that has one child then we we make a link or connection between the the child and parent of node to be deleted and after that we delete that node.
Example – In the above tree node 3 has one child, i.e. node 7. If we want to delete node 3, node 3 will be replaced by it’s one and only child node 7. i.e. 20 will be replaced by 25.
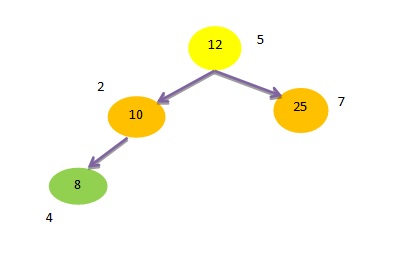
Case 3 : If The node to be deleted has Two children’s
Concept – If the node to be deleted has two children’s then we can use any one among two methods in this case.
Method 1 – Swap the node to be deleted by its in In Order predecessor after that node to be deleted become the leaf node than we can simply delete it.
Example – Here we want to delete 15 (node 1).
In the left sub tree, node 5 (12) is the largest. Hence 15 will be swap by node 12 After that we delete node 15. The result is shown below-
Method 2 –Swap the node to be deleted by its in In Order successor after that node to be deleted become the leaf node than we can simply delete it.
Example – If want to delete node 15 than Here there is just one element in the right sub tree, i.e. 25. Hence 15 (node 1) is to be replaced with 25 (node 7). The result is shown below.
Conclusion and Summary
In this Binary Search Tree tutorial we have learned the following concepts of binary search tree
- Introduction of Binary Search Tree
- Construct a binary search tree or insert a node in binary tree.
- Deletion of a node in Binary Tree.
In the next tutorial we will also learn about the types of binary search tree.
I hope that this tutorial will be beneficial for computer science students. Your feedback is precious to us. Please give your feedback or leave a comment to improve the quality of our tutorials and provide tutorials as per your expectation.
If you find this page helpful, then please Like and Share the post on Facebook, Twitter, LinkedIn through their icons as given below.