Prim’s Algorithm to find MST

Prim’s algorithm is a greedy algorithm used to find the minimum spanning tree in a given Graph. Problem based on Prim’s algorithm is mostly asked in GATE(CS/IT) Exam. Students preparing for GATE and UGC NET exam.

We have explained the Prim’s Algorithm to find minimum cost spanning tree with Example

Let’s understand prim’s algorithm with an example.

Example of Prim’s Algorithm to find MST

In this example we use Prim’s algorithm to find a minimum spanning tree mst for the given weighted graph.

Find the MST of the given graph using Prim’s algorithm.

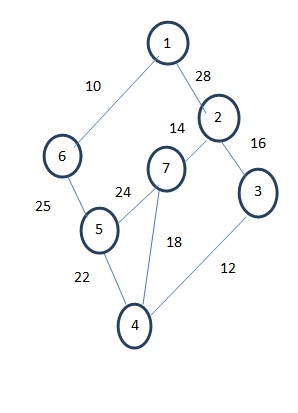
In the above graph adjacent vertices are (1,6),(1,2),(2,7)(2,3)(7,5)(7,4)(6,5)(5,4)(3,4) and number of vertices are 7.

Minimum weight is 10 and minimum weight edge is the edge that connect to vertex 6 and vertex 1.

Prim’s algorithm to find the minimum cost of spanning tree is given below-

Step 1 – In First step we select the edge with smallest edge cost.

Step 2- In second step we select the connected edges with the smallest cost.

Key Point to Remember – Key point to remember about prim’s algorithm is that prim’s algorithm treats the nodes as a single tree and after that keeps on adding new nodes to the spanning tree from the given graph to find the minimum cost.

For the example given above we have solved the questions using prim’s algorithm in following way.

The edge with the smallest cost is the edge from 6 to 1 (cost=10). Then we need to find out the connected edge with the smallest cost. There are two edges connected, one is 1 to 2 (cost=28) and another is 6 to 5 (cost=25).

Hence we choose the one with minimum cost (6 to 5). Similarly edge 5 to 6 is with cost 22 is minimum. Again, edge 4 to 3 with cost 12, 3 to 2 with cost 16 and 2 to 7 with cost 14 is selected which are with minimum cost. Hence the resultant MST is-

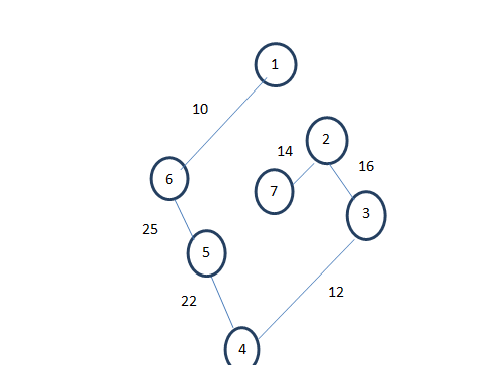
The total cost of the tree is= 10+25+22+12+16+14=99.

This minimum spanning tree includes every vertex of the graph.

Hence the above tree is the resultant minimum spanning tree with cost 99.

Note: If we have two graphs which are not connected to each other, no algorithm can find the MST from those two.

Time Complexity of Prim’s Algorithm

The time complexity of Prim’s Algorithm to find mst is O(VlogV + ElogV) = O(ElogV). Where V represents to Vertex of Graph and E is the Edge of the graph.