Table of Contents
Kruskal’s Algorithm and Example
Kruskal’s Algorithm in data structure is another greedy approach used to find the cost of spanning tree. Generally it is used to find the minimum spanning tree in the given Graph. Problem based on Kruskal’s algorithm is generally asked in GATE(CS/IT) and UGC NET exam.
In this tutorial we have explained the Kruskal’s Algorithm with example and solution step wise step. After reading this Kruskal’s algorithm in data structure tutorial students will be able to solve the minimum spanning tree based problems came in previous GATE exam.
Let’s try to understand Kruskal’s algorithm and with the help of an example.

Kruskal’s Algorithm Example
Problem – Find the MST of the given graph using Kruskal’s algorithm.
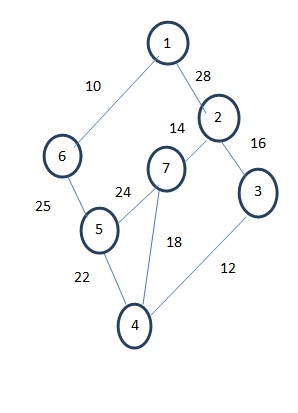
Solution
Kruskal’s algorithm says
(1) Always connect the edge with the smallest cost.
By following the algorithm, the first edge with the smallest edge is from 1 to 6 (cost=10). Then 3 to 4 (cost=12). Then 2 to 7 (cost=14).
(2) Then 2 to 3 (cost=16).
(3) Then we should select 7 to 4 (cost=18); but it would form a cycle as shown in figure below
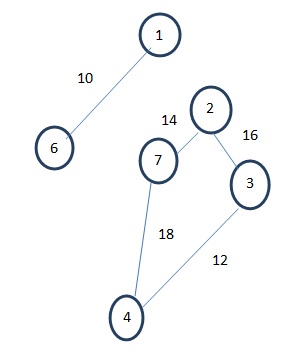
But according to the properties of spanning tree, a spanning tree can’t form a cycle. Hence the edge 7 to 4 can’t be selected and the edge 7 to 4 with cost 18 is discarded.
(4) Now we’ll find the next edge with the minimum cost which is 4 to 5 (cost=22). The next edge with minimum cost is 5 to 7 (cost=24).
But again it’ll construct a cycle as shown below-
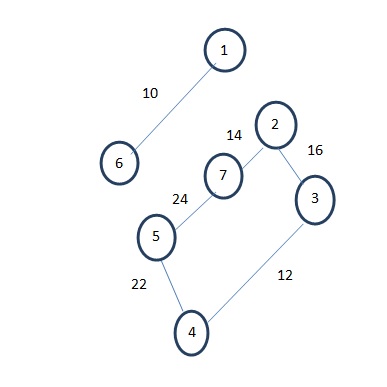
As a spanning tree can not contain a cycle, the edge 5 to 7 (cost=24) will be discarded and the next edge with minimum edge is selected which is 5 to 6 (cost=25).
Hence, the resultant MST will be as shown in following figure.
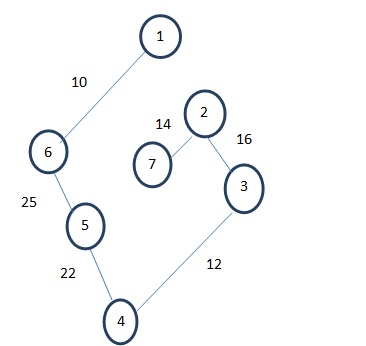
(5) The total cost of the tree is= 10+25+22+12+16+14=99.
If there are V no. of vertices and |E| no. of edges in a graph, the spanning tree of the graph will be formed only after connecting |V|-1 no. of edges.
Conclusion and Summary
In this Kruskal’s Algorithm in data structure tutorial we have explained the Kruskal’s Algorithm with example and solution. I hope that this algorithm will be beneficial for computer science students in solving the minimum spanning tree problem.
Previous Tutorial – Prim’s Algorithm for Graph Traversal
Next Tutorial – Hashing Tree in Data Structure


