Breadth First Search Algorithm

The Breadth First Search algorithm is a systematic search algorithm for graph or tree data structures. Breadth-first Search is sometimes also known as breadth-first traversal.

Questions based on the Breadth First Search algorithm are generally asked in the GATE(CS) and UGC NET exams every year. GATE and UGC aspirants are suggested to prepare this topic very well.

Today in this BFS Tutorial, we will learn the steps of the BFS algorithm, the implementation of the BFS algorithm in C Programming. and some basic concepts. We will also see an example of graph traversing using the BFS algorithm.

Let’s start with the introduction of BFS.

What is BFS Search Algorithm ?

BFS is a powerful technique of systematically traversing the number of edges of a given graph such that every edge is traversed once and also each vertex is visited at least once.

In breadth-first search algorithm used for Graph and Tree data structure, we’ll start from one vertex, and then we’ll visit all the adjacent vertices of that vertex.

Once we’re done exploring the first vertex, we’ll then start exploring other vertices that have not been visited.

Breadth First Search Algorithm effectively visits and marks all the key nodes in a Graph in a Breadthwise manner.

This algorithm selects a single node, mark it as visited and then visits all the nodes adjacent to selected nodes. This process will continue until all the nodes in the Graph are visited.

In context to Breadth First Search Algorithm, this is important to note that once the algorithm visits and marks the starting node, then it moves towards the nearest unvisited nodes and analyses them. Once visited, all nodes are marked.

These repetitions continue until all the nodes of the Graph have been successfully visited and marked.

To understand the breadth-first search algorithm, let’s take a simple example.

Breadth First Search (BFS) Algorithm Steps

Various steps of BFS algorithm are given below –

Step 1: Start

Step 2: Select the starting vertex form Graph and insert it into queue

Step 3: Find the vertices that have direct edges with the vertex it means vertex which is at the front of the queue.

Step 4: Insert all the vertices found in step 3 into queue

Step 5: Remove the first vertex in queue

Step 6: Continue this process until all the vertices are visited

Step 7: Stop

 

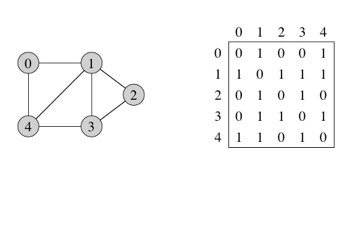
Consider the above Graph and it’s adjacency matrix. The BFS Traversal for above Graph when starting vertex is 0 will be 0 1 4 2 3.

Breadth First Search Program in C

#include<stdio.h>
#include<conio.h>

int a[20][20],q[20],visited[20],n,f=-1,r=-1;

void bfs(int v)
{
int i;
for (i=0;i<n;i++) // check all the vertices in the graph
{

if(a[v][i] != 0 && visited[i] == 0) // adjacent to v and not visited
{

r=r+1;

q[r]=i; // insert them into queue

visited[i]=1; // mark the vertex visited

printf(“%d “,i);

}

}

f=f+1; // remove the vertex at front of the queue

if(f<=r) // as long as there are elements in the queue

bfs(q[f]); // peform bfs again on the vertex at front of the queue

}

main()
{

int v,i,j;

printf(“\n Enter the number of vertices:”);

scanf(“%d”,&n);

for (i=0;i<n;i++) // mark all the vertices as not visited

{

visited[i]=0;

}

printf(“\n Enter graph data in matrix form:\n”);

for (i=0;i<n;i++)

for (j=0;j<n;j++)

scanf(“%d”,&a[i][j]);

printf(“\n Enter the starting vertex:”);

scanf(“%d”,&v);

f=r=0;

q[r]=v;

printf(“\n BFS traversal is:\n”);

visited[v]=1; // mark the starting vertex as visited

printf(“%d “,v);

bfs(v);

if(r != n-1)

printf(“\n BFS is not possible”);

getch();

}

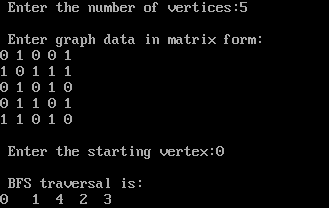
Output

Breadth First Search Example

Let’s understand breadth first search with an example. Consider the Graph as shown in following figure.

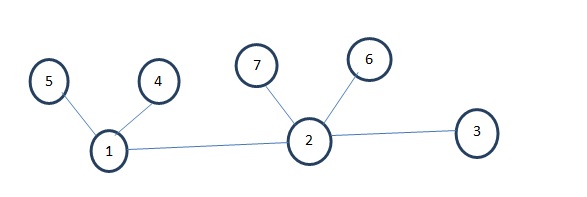
At first let’s visit the vertex 1. After visiting vertex 1, we’ll start exploring the vertex 1, i.e. start visiting all the adjacent vertices of 1. The adjacent vertices of 1 are 5, 4 and 2. We can visit the vertices in any order.

Then as vertex 2 is already visited, we’ll explore vertex 2. The adjacent vertices of 2 are 7, 6, 3. We can visit these vertices in any order.

The resultant BFS is 1, 2, 4, 5, 3, 6, 7.

Let’s take another simple example to understand breadth first search algorithm.

Consider the Graph as shown in following figure.

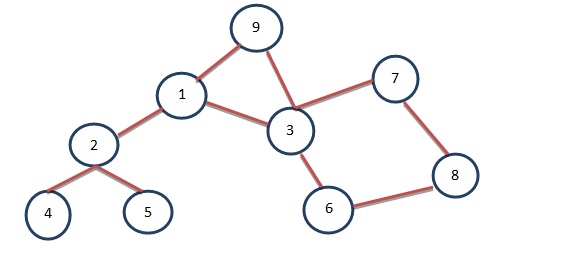
We’ll first visit vertex 1. Then let’s explore vertex 1. The adjacent vertices of vertex 1 are 2, 3 and 9. Hence we’ll visit 2, 3 and 9 which gives the following-

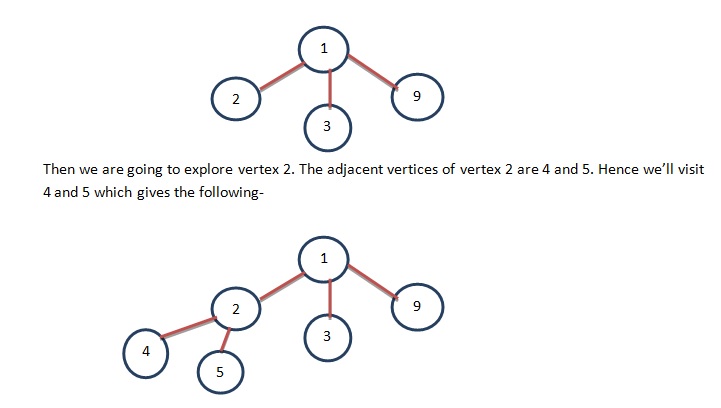
Then we are going to explore vertex 3. Vertex 3 is already visited and the adjacent vertices of vertex 3 are 6, 7 and 9. Vertex 9 is already visited. Hence we’ll visit 6 and 7 which gives us the following-

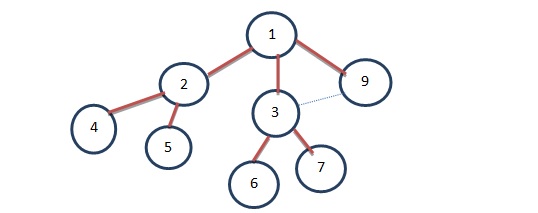
Then there is no adjacent vertex of the vertex 4 and 5 and those vertices are already visited. Vertex 6 is already visited and we are going to explore vertex 6.

Vertices 3 and 8 are adjacent to vertex 6. As vertex 3 is already visited, we’ll then visit vertex 8. Then we’ll explore vertex 7 whose adjacent vertices are 3 and 8. Both of them are already visited which gives us the following-

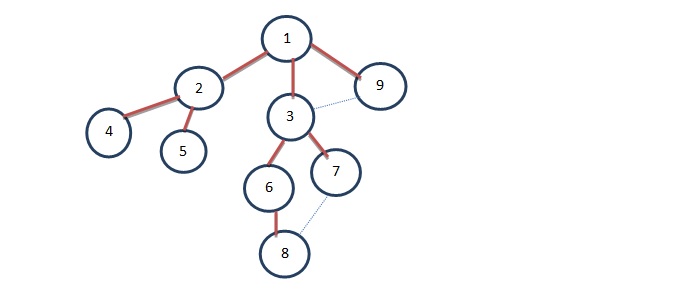
This resultant tree is called the BFS spanning tree. The dotted lines in the BFS spanning tree are called as Cross Edges.

The resultant BFS is 1, 2, 3, 9, 4, 5, 6, 7, 8

Why do we need Breadth First Search Algorithm ?

There are various uses of the breadth-first search algorithm.

• Breadth First search algorithm is useful in analyzing the nodes in a graph and finding the shortest path of traversing.
• It uses traverse in a small number of iterations.
• The accuracy of the Breadth First Algorithm is high as compared to other algorithms.

BFS Search Time Complexity 

The Time complexity of BFS or breadth first search is O(V + E) when Adjacency List is used and O(V^2) when Adjacency Matrix is used, where as per notation V stands for vertices and E stands for edges of the given graph.

Rules of BFS Algorithm

Some rules of BFS algorithm are given below –

A queue (FIFO-First in First Out) data structure is used by BFS.

You mark any node in the graph as root and start traversing the data from it.

• BFS traverses all the nodes in the graph and keeps dropping them as completed.
• BFS visits an adjacent unvisited node, marks it as done, and inserts it into a queue.
• Removes the previous vertex from the queue in case no adjacent vertex is found.
• BFS algorithm iterates until all the vertices in the graph are successfully traversed and marked as completed.
• There are no loops caused by BFS during the traversing of data from any node.

Applications of BFS Algorithm.

Some real life example of BFS Algorithm are as follow –

Un-weighted Graphs

BFS algorithm can easily find the shortest path and a minimum spanning tree to visit all the vertices of the graph in the shortest time with high accuracy.

P2P Networks

BFS can be implemented to locate all the nearest or neighboring nodes in a peer to peer network. This will find the required data faster.

Web Crawlers

Search engines or web crawlers can easily build multiple levels of indexes by employing BFS.

BFS implementation starts from the source, which is the web page, and then it visits all the links from that source.

Navigation Systems

BFS can help find all the neighboring locations from the main or source location.

Network Broadcasting

A broadcasted packet is guided by the BFS algorithm to find and reach all the nodes it has the address for..

Conclusion and Summary

Breadth first search is an important approach used for graph search. We have explained breadth first search method with example. I hope after reading this BFS search algorithm tutorial you will be able to attempt the BFS based questions.

If you have any query related to BFS Graph Search algorithm then feel free to ask in comment section.

Previous Tutorial – Types of Hashing in Data Structure

Next Tutorial – Depth First Search Algorithm for Graph