Table of Contents
Merge Sort and It’s Time Complexity
Merge sort and it’s time complexity make it more useable sorting algorithm in Data structure. In this article we will discuss about Merge Sort algorithm and it”s time complexity.
Questions based on merge sort are generally asked in GATE(CS) and UGC NET exam.
In this tutorial we will discuss merge sort algorithm, merge sort times complexity and we will also learn about working of merge sort algorithm along with merge sort program in C Programming Language
So let’s start with introduction of merge sort algorithm.
What is Merge Sort Algorithm ?
- Merge sort is a Sorting Techniques that follow Recursive and Divide and Conquer Approach.
- The divide and conquer strategy says that if a list is large then divide the complete list into sub-lists.
- We’ll keep dividing the list into sub-lists until each sub-list is having one element. Then we’ll merge the sub-lists into one list until we have a sorted list.
Pseudo Code for Merge Sort Algorithm is given below
In the following algorithm, ar is the given array, begin is the starting element, and ends is the last element of the array.
MERGE_SORT(ar, begin, ends)
if begin < ends
set mid = (begin + ends)/2
MERGE_SORT(ar, begin, mid)
MERGE_SORT(ar, mid + 1, ends)
MERGE (arr, begin, mid, ends)
end of if
END MERGE_SORT
MERGE function written in above pseudo code is an important part of merge sort algorithm.
This MERGE unction performs the merging of two sorted sub-arrays that are Ar[begin…mid] and Ar[mid+1…ends] and build one sorted array A[begin…ends]s. A[], begin, mid, and ends are the input of merge function,
The implementation of the MERGE function in c programming is given as follows –
void mergesort(int ar[], int begin, int mid, int ends)
{
int a,b, c;
int n1 = mid – begin + 1;
int n2 = ends – mid;
int LeftArray[n1], RightArray[n2]; // these are temporary arrays
/* now copy data item to these temp arrays */
for (int a= 0; a < n1; a++)
LeftArray[i] = ar[begin + i];
for (int b = 0; b < n2; b++)
RightArray[j] = ar[mid + 1 + j];
a= 0, /*this is initial index of first sub-array */
b= 0; /*this is initial index of second sub-array */
c = begin; /*this is initial index of merged sub-array */
while ( a< n1 && b< n2)
{
if(LeftArray[a] <= RightArray[b])
{
ar[c] = LeftArray[a];
a++;
}
else
{
ar[c] = RightArray[b];
b++;
}
c++;
}
while (a<n1)
{
ar[c] = LeftArray[a];
a++;
c++;
}
while (b<n2)
{
ar[c] = RightArray[b];
a++;
c++;
}
}
Working of Merge Sort Algorithm Example
Let us try to understand the working of merge sort algorithm with a simple example-
Consider an Array Data Structure A given below . Array consist 8 elements which are in unsorted order. Now we have to sort this array in increasing order using merge sort algorithm.
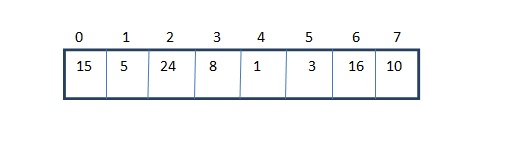
Step 1 – First we’ll divide this array into two equal sub arrays.
Step 2- First we need to find out the mid position of the array and we’ll divide the array from the mid position. Here mid position would be
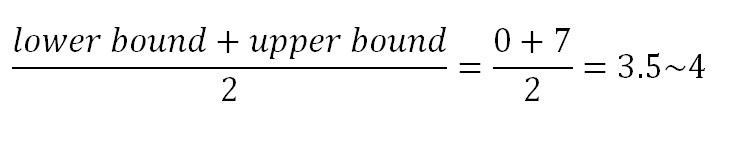
Hence from position 0 to 4, we have one sub list and from 5 to 7another sub list.
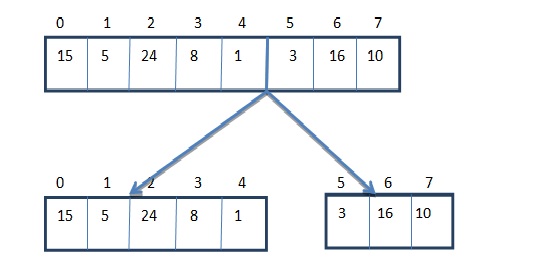
Step 3 – Again we’ll divide both the left and the right sub list into two sub lists again.
Step 4 – We’ll keep dividing until we find a sub list with only one element. In the left sub list the mid element is 0+4/2=2nd position.
In the right sub list the mid element is 5+7/2=12/2=6th position.
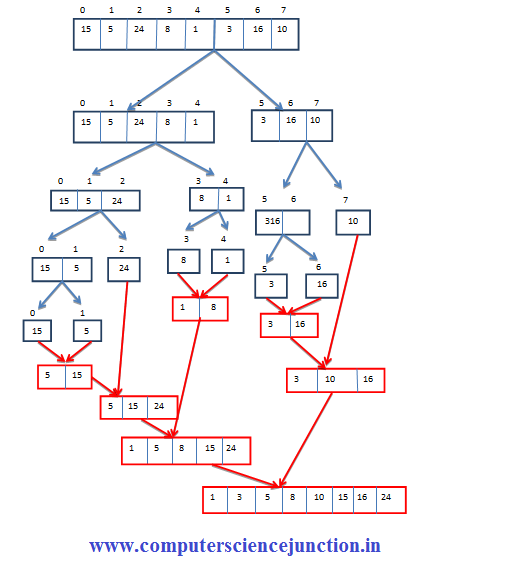
We can’t further divide the sub lists when each sub list will have only one element.
Then we are going to merge these sorted sub lists which will again produce a complete sorted list.
Point To Remember – If there is ‘m’ no. of elements in the left sub list and ‘n’ elements in the right sub list, time complexity of merging these sub lists is Θ(m+n).
- If we denote left sub list as ‘L’ and the right sub list as ‘R’, then while merging these two sub list we need to compare 1st element of L with 1st element of R; i.e. we need to compare Li with Rj.
- The element which is the smallest will come first and we’ll keep comparing elements till we get a sorted list.
- Whole process of merge sort algorithm discuss in above steps is as shown in Figure.
Merge Sort’s Time complexity
For n no. of elements in an array time taken by a merge sort algorithm is Θ(n Log(n)).
Merge Sort Program in C
Some time in Technical Interview , along with Merge Sort and it’s time complexity interviewer also ask to write a prom in c for merge sort. So in this section we are going to tell you how to write a merge sort program in c to implement the merge sort algorithm.
Students are requested to run this c program and perform the merge sort.
#include <stdio.h>
#include<conio.h>
/* first we implement Function to merge the subarrays of a[] */
void merge(int a[], int begin, int mid, int ends)
{
int i, j, k;
int m1 = mid – begin + 1;
int m2 = ends – mid;
int LFA[m1], RA[m2]; //LFA is Left Array and RA is RightArray , these are temporary arrays
/* copy data to temp arrays */
for (int i = 0; i < m1; i++)
LFA[i] = a[begin + i];
for (int j = 0; j < m2; j++)
RA[j] = a[mid + 1 + j];
i = 0; /* initial index of first sub-array */
j = 0; /* initial index of second sub-array */
k = begin; /* initial index of merged sub-array */
while (i < m1 && j < m2)
{
if(LFA[i] <= RA[j])
{
a[k] = LFA[i];
i++;
}
else
{
a[k] = RA[j];
j++;
}
k++;
}
while (i<m1)
{
a[k] = LFA[i];
i++;
k++;
}
while (j<m2)
{
a[k] = RA[j];
j++;
k++;
}
}
void mergeSort(int a[], int begin, int ends)
{
if (begin < ends)
{
int mid = (begin + ends) / 2;
mergeSort(a, begin, mid);
mergeSort(a, mid + 1, ends);
merge(a, begin, mid, ends);
}
}
/* Function to print the array */
void printArray(int a[], int n)
{
int i;
for (i = 0; i < n; i++)
printf(“%d “, a[i]);
printf(“\n”);
}
int main()
{
int a[] = { 12, 31, 25, 8, 32, 17, 40, 42 };
int n = sizeof(a) / sizeof(a[0]);
printf(“Enter the array elements – \n”);
printArray(a, n);
mergeSort(a, 0, n – 1);
printf(“Array elements after sorting are – \n”);
printArray(a, n);
return 0;
}
Output
When we will run the above program then we will get the following output.
Enter the array elements
15 16 2 19 35 26 21 4
After Sorting Array element s are
2 4 15 16 19 21 26 35
Conclusion and Summary
- I hope after reading this merge sort and it’s time complexity tutorial students will be able to do the problem based on merge sort.
- Students can apply the merge sort concepts in sorting the data.
- We have also discussed the merge sort program in c
If you have any query regarding the merge sort and it’s time complexity related this article then you may ask in comment section.


