Compiler Design GATE Questions for Practice

Compiler Design GATE Questions for practice are explained in this tutorial. Compiler Design is and important subject for GATE(CS/IT) and UGC NET exam.

Compiler design mcq for GATE exam explained  in this tutorial will be beneficial for GATE aspirants. So they are requested to practice these questions very well.

Table of Content

In this tutorial we have discussed the compiler design GATE questions from these topics.

• LR Parsing
• First Follow
• SDT
• Grammar

Compiler Design GATE Questions for Practice SET1

 S → aSAb | bSBc ⇨First(S) = {a, b}

A → +AB | ε ⇨First(A) = {+, ε}

B → *BC | ε ⇨First(B) = {*, ε}

C → aC | d ⇨First(C) = {a, d}

Q1. For the above What is in the Follow(S)?

(a) {a, b, c, +, $} (b) {a, c, +, *, $}

(c) {b, c, +, *, $} (d) {a, b, d, *, $}

 Solution: Option (c)

 Explanation

S → aSAb | bSBc

A → +AB | ε

B → *BC | ε

C → aC | d

Follow(S) = {First(A), First(B), b, c, $}

 Q2. What is in the Follow(B)?

(a) {a, b, c, d, *} (b) {a, b, d, ε, $}

(c) {a, c, d, *, $} (d) {c, d, b, +, *}

Solution: Option (a)

Explanation

Follow(B) = {C, Follow(A), First(C)}

b, First(B)

= {c, b, *, a, d} 2

Q3.  Which among the following is false.

(a)  LL(1) Grammer can not be recursive or ambiguous.

(b) LR method of parsing produced the Grammar which is a proper subset of the grammar produced by LL method.

(c) LR parsing is non-backtracking method

(d)  LL Method of  parsing generate less language than LR method.

Solution: Option (b)

Explanation

FALSE, as LL(1) ⊆ LR(k)

Q4. Consider the following SDT.

A → BC *(I) B.i = f(A.i)

(II)  B.i = f(A.S)

(III)  A.S = f(B.s)

L attributed meaning is violated by which of the above ?

(a) I only (b) II only

(c) I, II (d) I, II, III

Solution: Option (b)

Explanation

It does not follow L-attribute definition.

Q5. Consider the following –

X → YZ

Y → Y + Z {print (‘+’);}

T {Y.val = T.val}

Z → *Y {print (‘*’);} Z

T {Z.val = T.val}

ε

T → num {print(num.val);} 3

Q6. For 2+3*2, the above translation scheme prints

(a) 2+3*2 (b) 23+2*

(c) 232*+ (d) 23*2+

Solution: Option (b)

Explanation

23 + 2*

Q7. Consider the following expression

x = a*b – c*d+e

The number of registers excluding the Accumulator required to generate the target code will be ?

(a) 1 (b) 2

(c) 3 (d) 5

Solution: Option (a)

Explanation

x = a * b – c * d + e

MOV A, a

MUL b

MOV R1, A

MOV A, C

MUL d

SUB R1, A

ADD R1, e

So, One Register required. 4

Q8. Consider the following two grammars

G1: A → A1 | 0A1 | 01

G2: A → 0A | 1

Select the Correct Option among the following –

(a) L1 is LR(k) (b) L2 is LR(k)

(c)  L1 and L2 are LR(k) (d) No one is LR(k)

Solution: Option (b)

Explanation

Since  G1: A → A1 | 0A1 | 01 — Ambiguous grammar

Since   G2: A → 0A | 1 — Regular grammar

Ambiguous grammar is not LR(k)

Above Regular grammar is LR(k)

Q9. Consider the following grammar.

S → aB | aAb

A → bAb | a

B → aB | ε

If we want to generate the string aab from the above grammer then how many  back tracks  we need?

(a) 1 (b) 2

(c) 3 (d) 4

Solution: Option (b)

Explanation

S ⇨ aB S ⇨ aAb S ⇨ aAb

⇨ aaB ⇨ abAbb ⇨ aab

⇨ aa ⇨ ababb

 Backtrack Backtrack

So, 2 backtracking is required.

Q10. For the given expression tree if on the machine load-store architecture where memory can be accessed only through load and store instructions. Suppose three variables a, b, c, d and e initially stored in memory. The binary operators used in this expression tree can be evaluate by the machine only when the operands are in Registers. Assume that instructions produce results only in a register and no intermediate results can be stored in memory. For this scenario find the minimum number of registers needed to evaluate this expression ?    [GATE 2011]

(a) 2

(b) 3

(c) 9

(d) 6

 

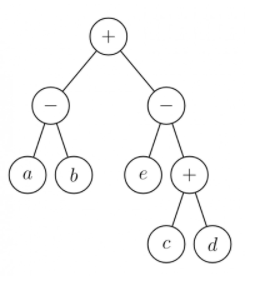
Answer : Option B is right.

Total 3 register are needed.

Explanation

R1←c,
R2←d,
R2←R1+R2,
R1←e,
R2←R1-R2

No R2 conatains the result of right sub tree and we can make empty to R1

Now to solve the left sub tree we can use R1 first to store the a and take a new register R3 to store the b.
it means

R1←a,
R3←b,
R1← R1-R3

Now register R1 is empty

So result of overall expression is R1+R2

R1← R1+R2

Conclusion and Summary

In this tutorial we have explained the Compiler Design GATE questions or GATE questions on Compiler Design for practice. These compiler design MCQs for GATE will be beneficial for computer science students.