Infix to Postfix Conversion using Stack Example

Infix to postfix conversion using stack examples with answers are explained here in this tutorial.

Infix to postfix conversion using stack based problem solving questions are generally asked in university examination and also in competitive examination.

Today in this tutorial we have  discussed the procedure to convert a given infix expression to postfix form with example.

Algorithm to Convert Infix to Postfix Conversion 

Before study of infix to postfix conversion using stack with examples with answer we should have knowledge about the Operator Precedence. In an infix expression generally following operators are used.

Addition     +

Subtraction   –

Multiplication  *

Division     /

Power (exponent) operator    ^

Modulus Operator %

Parenthesis ( )

Precedence order  (  ) > ^ > *, / ,%  >  +, –

Parenthesis operator has highest precedence after that power operator then multiplication and division operator  and addition and subtraction has least precedence.

Here it is important to note that * , %  and / has equal precedence. Similarly + and – operator has equal precedence.

Stack is used to convert a given infix expression to postfix form. We use the following steps to convert a given infix expression to postfix form.

Step 1 –  Scan each character in given infix expression one by one from left to right till end.

Step 2 – If the scanned character is operand then put it into Postfix String

Step 3 – If the scanned character is an operator then do the following –

        Case 1– IF there is no operator is present on stack then push the currently scanned operator on stack.

 Case 2 – IF there is an operator is already present at the top of stack that has the lesser precedence than the currently scanned operator then also push the currently scanned operator on the top of stack.

Case 3 – IF there is an operator is already present at the top of the stack that has the greater or equal precedence than the currently scanned operator then POP that operator from stack and append that operator to the postfix sting and push the currently scanned operator on the top of stack.

Step 4 – IF left and right parenthesis is occurred then push it on stack.

Step 5 – IF there is a case when some operators are enclosed between left parenthesis and right parenthesis on stack then pop the enclosed operators one by one from up to down and append to postfix string. here left and right parenthesis will cancel to each other they will not be append to postfix string.

Infix to Postfix Conversion Example 

Example 1 – Convert the following infix expression to postfix form

A + B * C – D / E  * H

Solution 

Solution of above question is given in following image.

Example 2 – Convert the following infix Expression to Postfix form

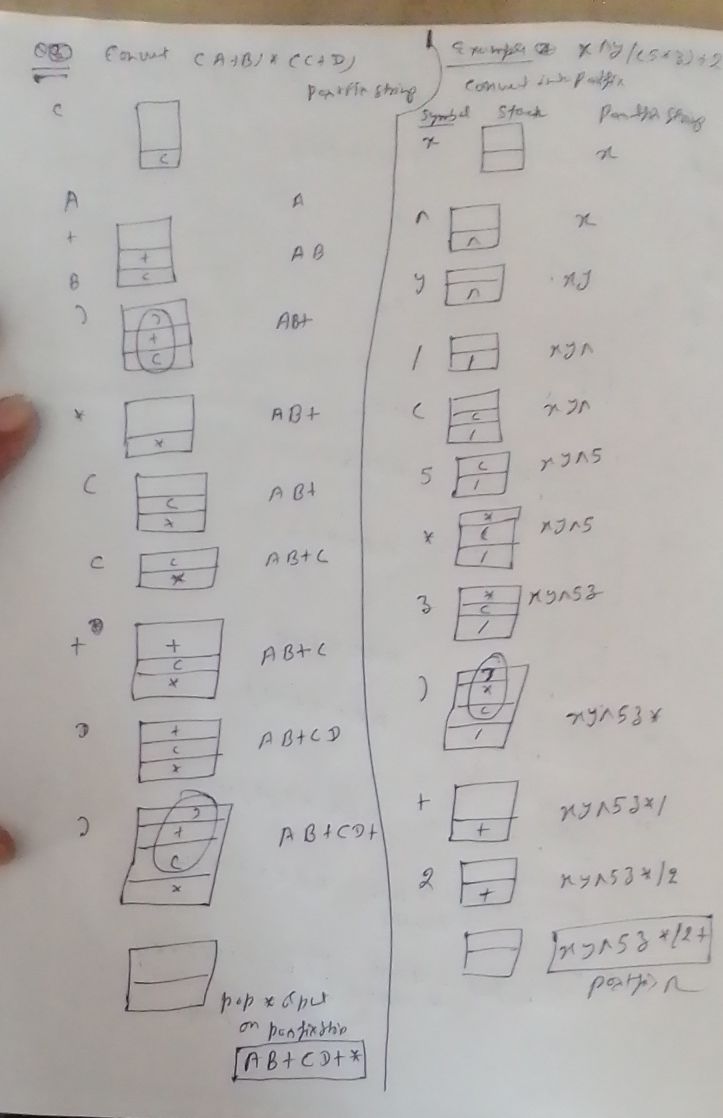
                        ( i )    ( A + B) * ( C + D)

                         ( ii )  X ^ Y / ( 5 * Z ) + 2

Solution 

Solution of the above questions are explained in the following image.

Example 3 – Convert the following infix expression to postfix form

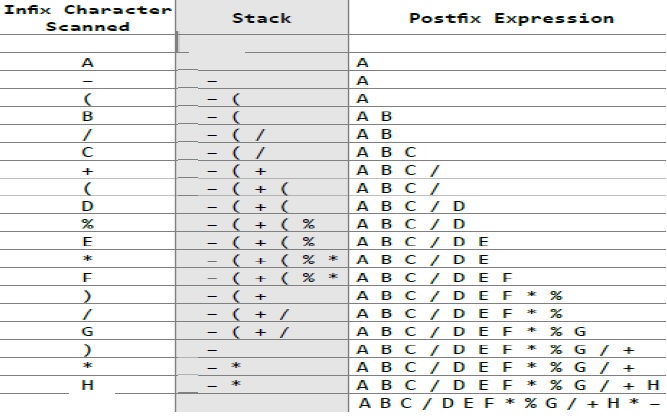
 A – ( B / C +  ( D % E * F ) / G ) * H

Solution – Infix to Postfix conversion of the above question is explained in the following image.

Infix to Postfix Conversion Problems

Various problems based on Infix to Postfix conversion are given in this section. These problems are also asked in AKTU University Data Structure Examination in previous year.

Q1. Convert A-B/C+D*E+F  into its equivalent  postfix [ AKTU 2017-18] .

Q2. Convert the given Infix expression to equivalent Postfix [ AKTU 2017-18]

                   A + (B * C – ( D/E ^ F) * G ) * H

Q3. Consider the following infix expression and convert into reverse polish  notation ( Postfix) using stack.  A + (B * C – (D / E ^ F) * H)       [ AKTU 2018-19]

Students can solve these questions as per the process explained in this tutorial.

Conclusion and Summary

• In the is tutorial we have explained the algorithm to convert a given infix to postfix conversion with examples using stack form with example.
• Problems based on infix to postfix conversion are solved with example in step wise step manner.
• We have also discussed the Infix to Postfix Conversion problems asked in Data Structure AKTU Examination.