Floyd Warshall Algorithm Example

Floyd warshall algorithm example in C or Data structure is used to find the all pairs shortest path it means shortest path among all the vertices pairs in a given weighted graph.

In this tutorial we have explained the floyd warshall algorithm example.

Frequently asked Questions

Some frequently asked questions are as follow

What is Floyd Warshall Algorithm ?
How does Floyd Warshall algorithm work ?
What is difference between Floyd Warshall and Dijkstra Algorithm ?

What is Floyd Warshall Algorithm ?

Floyd warshall algorithm is used to find the all pairs shortest path in a given weighted graph.
Floyd warshall algorithm in C Language uses each vertex of the graph as a pivot to check if it provides the shortest way to travel from one point to another.
Floyd warshall algorithm is applicable on both directed graph and undirected graph.

How does Floyd Warshall algorithm work ?

Floyd warshall algorithm in data structure works using the following steps.

Step 1- Construct an adjacency matrix A that will contains all cost of edges present in the graph. If there is no direct edge be

Step 2- Compute another matrix A1 from A keeping the first row and first column of the roiginal adjacency matrix as in A1and for remaining values say A1[i,j] if A[i][j] > A[i,k]+A[k,j] then replace A1[i,j] with (A[i,k]+A[k,j]) otherwise dont change the value. Here in this step k=1 when first vertex is the selected as pivot.

Step 3- Repeat Step 2 for all the vertices in the graph by changing the value of K for every pivot vertex until the final matrix is achieved.

Step 4- The final adjacency matrix obtained is the final solution with shortest path.

Floyd Warshall Algorithm Example

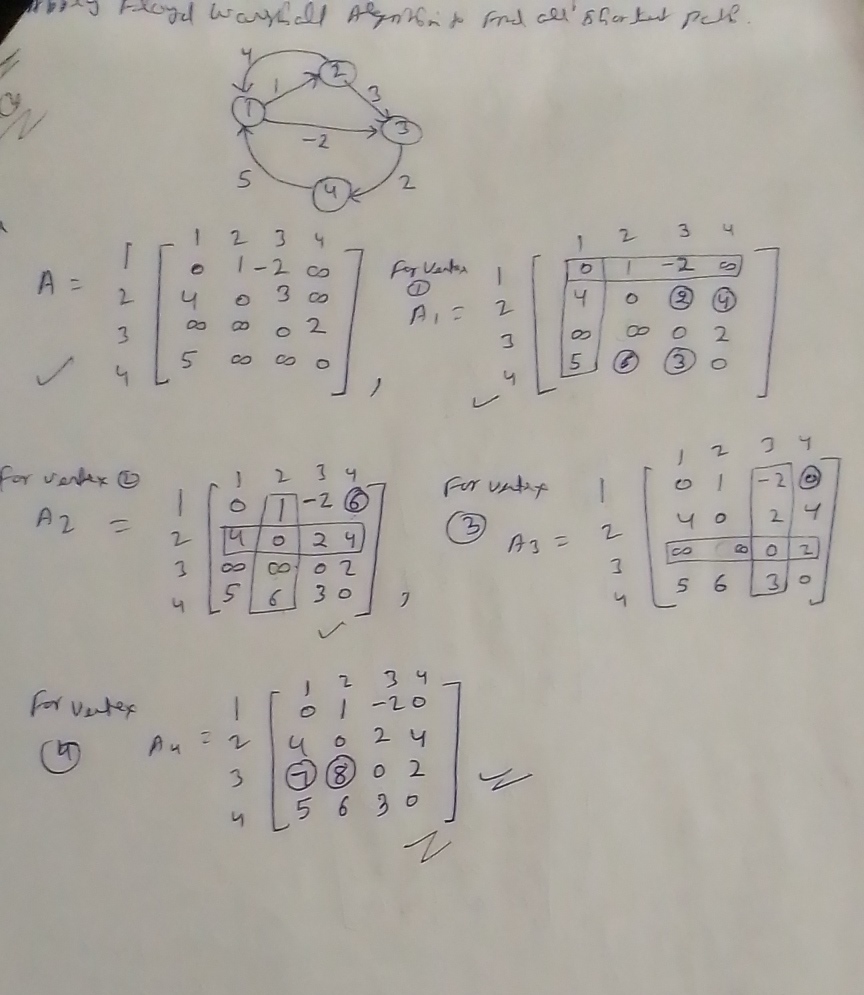
Question1. Consider the weighted Graph as shown in following Figure. We have to find the all pairs shortest path using Floyd Warshall algorithm in the given weighted graph.

Problem based on Floyd Warshall algorithm is solved step wise step in the above picture.

First we calculate the Adjacent Matrix from the given graph. Then by following the steps 2 to step 4 we computed the matrix for each vertex of the graph. The final matrix D4 represents the all pairs shortest path.

Infinity value in Matrix D4 represents that no path exist between corresponding vertices.

Question 2 – In the given graph find all pairs shortest path using Floyd Warshall Algorithm.

Conclusion and Summary

In this post we have discussed and explained the Floyd Warshall Algorithm example and steps.
Problem based on Floyd Warshall algorithm is solved in step wise step manner.